LAS FRACCIONES
El ejemplo clásico es el de un queso que partimos en porciones. En el dibujo, hemos hecho 8 porciones, 3 rosas y 5 verdes.
| Si tomamos las 3 rosas, representan 3 porciones de las ocho en las que hemos dividido el queso, es decir 3 / 8 del queso, y si tomamos las 5 verdes, representan 5 porciones de las ocho en las que hemos dividido el queso, es decir 5 / 8 del queso. |
Las partes que tomamos ( 3 ó 5 ) se llaman numerador y las partes en que dividimos el queso ( 8 ) denominador.
Para leer una fracción, el numerador se lee normalmente pero, como veremos a continuación, el denominador tiene una forma especial de leerse.
| Denominador | Lectura | Ejemplos |
| 2 | medios | 5 / 2 = cinco medios |
| 3 | tercios | 2 / 3 = dos tercios |
| 4 | cuartos | 3 / 4 = tres cuartos |
| 5 | quintos | 4 / 5 = cuatro quintos |
| 6 | sextos | 5 / 6 = cinco sextos |
| 7 | séptimos | 6 / 7 = seis séptimos |
| 8 | octavos | 7 / 8 = siete octavos |
| 9 | novenos | 8 / 9 = ocho novenos |
| 10 | décimos | 9 / 10 = nueve décimos |
| mayor de 10 | Se agrega al número la terminación avos | 10 / 11 = diez onceavos |
Si en una fracción multiplicamos o dividimos el numerador y el denominador por un mismo numero, obtenemos una fracción equivalente a la primera, pues ambas tienen el mismo valor. Por ejemplo:
Simplificar o Reducir una fracción consiste en hallar la fracción equivalente más pequeña posible; para ello, lo primero que hacemos es buscar el mayor número que divide exactamente (resto = 0) al numerador y al denominador (mayor divisor común) y después dividimos el numerador y el denominador por este mayor divisor común, ya que como hemos visto antes, dividiendo el numerador y el denominador de una fracción por un mismo número obtenemos una fracción equivalente (de igual valor).
Por ejemplo: Simplificar 30/42
Los números que dividen exactamente a 30 (divisores) son: 2, 3, 5, 6, 10 y 15.
Los números que dividen exactamente a 42 (divisores) son: 2, 3, 6, 7, 14 y 21.
Los divisores comunes a ambos son 2, 3 y 6. El mayor divisor común es 6, por tanto, dividimos numerador y denominador por 6.
Cuando en una fracción, el numerador y el denominador no tienen ningún divisor común, se dice que es una fracción irreducible.
| 1 | (1 x 4) | 4 | 3 | (3 : 3) | 1 | |||||||||
| — | = | ——— | = | — | = | 0,5 ; | — | = | ——— | = | — | = | 0,2 | |
| 2 | (2 x 4) | 8 | 15 | (15 : 3) | 5 |
SIMPLIFICAR Y REDUCIR FRACCIONES
Simplificar o Reducir una fracción consiste en hallar la fracción equivalente más pequeña posible; para ello, lo primero que hacemos es buscar el mayor número que divide exactamente (resto = 0) al numerador y al denominador (mayor divisor común) y después dividimos el numerador y el denominador por este mayor divisor común, ya que como hemos visto antes, dividiendo el numerador y el denominador de una fracción por un mismo número obtenemos una fracción equivalente (de igual valor).
Por ejemplo: Simplificar 30/42
Los números que dividen exactamente a 30 (divisores) son: 2, 3, 5, 6, 10 y 15.
Los números que dividen exactamente a 42 (divisores) son: 2, 3, 6, 7, 14 y 21.
Los divisores comunes a ambos son 2, 3 y 6. El mayor divisor común es 6, por tanto, dividimos numerador y denominador por 6.
| 30 | 30/6 | 5 | ||
| —— | = | ——— | = | — |
| 42 | 42/6 | 7 |
Cuando en una fracción, el numerador y el denominador no tienen ningún divisor común, se dice que es una fracción irreducible.
Fuente: El abuelo educa
JUEGA CON PROBLEMAS DE FRACCIONES
LOS NÚMEROS MIXTOS
Un número mixto está formado por un número natural y una fracción. Todas las fracciones mayores que la unidad se pueden expresar en forma de número mixto.
Hay dos casos:
- Primero. Pasar de fracción a número mixto. Ejemplo 8/5. Se hace la división 8:5= 1 y el resto es 3. Por tanto: 1 es el número natural y 3 es el numerador de la fracción y le denominador no cambia, es decir 5.
- Segundo: Pasar de número mixto a fracción. El numero natural se multiplica por el denominador y se suma el numerador. Ejemplo 1 + 2/3. Operamos: 1X3 = 3+2 = 5
Practica un poco en los siguientes enlaces:
FRACCIONES EQUIVALENTES
Las Fracciones Equivalentes tienen el mismo valor, aunque parezcan diferentes.
Estas fracciones son en realidad lo mismo:
| 1 | = | 2 | = | 4 |
| 2 | 4 | 8 |
¿Por qué son lo mismo? Porque cuando multiplicas o divide a la vez arriba y abajo por el mismo número, la fracción mantiene su valor. La regla a recordar es:
¡Lo que haces a la parte de arriba de la fracción
también lo tienes que hacer a la parte de abajo!
Por eso, estas fracciones son en realidad la misma:
| × 2 | × 2 | |||
| 1 | = | 2 | = | 4 |
| 2 | 4 | 8 | ||
| × 2 | × 2 | |||
| 1/2 | 2/4 | 4/8 | ||
| = | = |
Aquí hay más fracciones equivalentes, esta vez dividiendo:
| ÷ 3 | ÷ 6 | |||
| 18 | = | 6 | = | 1 |
| 36 | 12 | 2 | ||
| ÷ 3 | ÷ 6 | |||
Si seguimos dividiendo hasta que no podamos más, habremos simplificado la fracción (la hemos hecho la más simple posible).
Importante:
- Las partes de arriba y abajo de la fracción siempre deben ser números enteros.
- Las operaciones que podemos hacer son multiplicar y dividir (siempre las dos partes a la vez). Si sumamos o restamos un número arriba y abajo, no tendremos una fracción equivalente.
- El número que elijas para dividir las dos partes no debe dejar ningún resto en las divisiones.
Practica un poco:
REDUCIR A COMÚN DENOMINADOR
¿ Qué significa y para qué sirve?
Reducir fracciones a común denominador significa encontrar fracciones equivalentes a las originales pero que tengan
el mismo denominador. Esto nos sirve para sumar, restar y comparar fracciones de una manera más fácil.
Reducir fracciones a común denominador significa encontrar fracciones equivalentes a las originales pero que tengan
el mismo denominador. Esto nos sirve para sumar, restar y comparar fracciones de una manera más fácil.
1. MÉTODO DE MÍNIMO COMÚN MÚLTIPLO.
2. MÉTODO DE PRODUCTOS CRUZADOS.
1. método de mínimo común múltiplo
Reducir dos o más fracciones a común denominador consiste en hallar fracciones equivalentes a las primeras con el mismo denominador.
Para reducir a común denominador:
1. Calcula el mínimo común múltiplo (m.c.m.) de los denominadores.
2. Divide el m.c.m entre cada denominador.
3. Multiplica cada fracción por el resultado de cada división
Para reducir a común denominador:
1. Calcula el mínimo común múltiplo (m.c.m.) de los denominadores.
2. Divide el m.c.m entre cada denominador.
3. Multiplica cada fracción por el resultado de cada división
2. MÉTODO DE PRODUCTOS CRUZADOS.
- Método de productos cruzados: Se multiplican los denominadores entre sí y después solo tenemos que
multiplicar los numeradores de antes por el denominador de la otra fracción. Así puede sonar muy lioso, pero
ya veras con este dibujo lo fácil que es.

ejercicios para prácticar método m.c.m.
- Método de productos cruzados: Se multiplican los denominadores entre sí y después solo tenemos que
multiplicar los numeradores de antes por el denominador de la otra fracción. Así puede sonar muy lioso, pero
ya veras con este dibujo lo fácil que es.
Practica un poco:
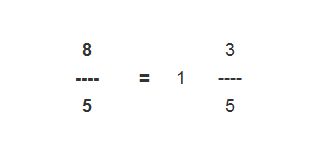
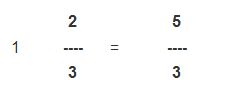


Seño soy ingrid gracias por ponernos ejercicios de mates me ayuda mucho praticar porque a veces tengo problemas
ResponderEliminarHola seño,me gusta mucho estos ejercicios de Matemáticas,por que me ayudan mucho a estudiar,voy a estudiar mucho para aprobarlo y practicare mucho para aprobarlo,gracias también por poner ejercicios y poner de tu parte ,te quiero mucho gracias:)de Lucía Medina Muñoz
ResponderEliminarSomos Kaleria y Victor nos ha gustado los juegos aunque, no lo hemos jugado todos pero, estan chulos y los videos, que nos han ayudado un poquito mas a comprender el tema .
ResponderEliminarHola somos Alicia , Lorena y Patricia. Hola soy Lorena he entendido muy bien gracias a los ejercicios y a mis compañeras .Somos Ali y Patri nos ha gustado poder ayudar a nuestra compañera y los ejercicios son muy educativos te queremos un beso
ResponderEliminarQue satisfacción que estos ejercicios os hayan sido de ayuda, gracias chic@s, sois estupendos.
ResponderEliminar